转载：功率谱学习及matlab代码_qinghuanduji的博客-程序员宝宝_功率谱matlab – 欧菲博客

转载：功率谱学习及matlab代码_qinghuanduji的博客-程序员宝宝_功率谱matlab

作者

前记

  • 只接触很少信号处理的问题，该篇是查阅资料总结的，先对概念等内容进行介绍，最后附matlab的功率谱代码。
  • 看了很多资料，没有说明白为啥可以有这么多种方法计算，也不清楚具体这种方法计算出来的是否正确，就写了一篇总结篇总结一下。

功率谱与频谱在计算上的区别

  • 功率谱：信号在自相关后FFT
  • 频谱：信号直接FFT

能量信号和功率信号的介绍

  • 二者的定义：
    • 能量信号：又称能量有限信号，是指在所有时间上总能量不为零且有限的信号。
    • 功率信号：它的能量为无限大，它对通信系统的性能有很大影响，决定了无线系统中发射机的电压和电磁场强度。
  • 二者的收敛性
    • 能量信号其傅氏变换收敛（即存在），而功率信号傅氏变换通常不收敛。（当然，若信号存在周期性，可引入特殊数学函数（Delta）表征傅氏变换的这种非收敛性）
  • 实际信号的介绍
    • 实际信号多为随机信号，这类信号的特点是状态随机性随时间无限延伸，其样本能量无限。换句话说，随机信号（样本）大多属于功率信号而非能量信号，它并不存在傅氏变换，亦即不存在频谱。
    • 实际中我们获得的往往仅仅是信号的一段，此时即使信号为功率信号，截断之后其傅氏变换收敛，但此变换结果严格来讲不属于任何“谱”（进一步分析可知它是样本真实频谱的平滑：卷积谱）；对上述变换若取其幅度平方，可作为平稳信号功率谱（密度）的近似，是为经典的“周期图法”；
  • 随机信号的介绍
    • 随机信号又称随机过程，很多噪声属于特殊的随机过程，它们的某些统计特性具有平稳性，其均值和自相关函数具有平稳性。对于这样的随机过程，自相关函数蜕化为一维确定函数，前人证明该确定相关函数存在傅氏变换。

概念解释

  • 功率谱定义及计算：
    • 一个是自相关函数的傅立叶变换；（维纳辛钦定理）
  • 另一个是时域信号傅氏变换模平方然后除以时间长度。（来自能量谱密度）
    • 信号的传播都是看不见的，但是它以波的形式存在着，这类信号会产生功率，单位频带的信号功率就被称之为功率谱。它可以显示在一定区域中信号功率随着频率变化的分布情况。
    • 注：根据parseval定理，信号傅氏变换模平方被定义为能量谱，能量谱密度在时间上平均就得到了功率谱。
  • 频谱的定义及计算：
    • 频谱是频率谱密度的简称，是频率的分布曲线。常常指信号的Fourier变换。

两者的联系与区别

  • 能量信号频谱通常既含有幅度也含有相位信息。
  • 幅度谱的平方（二次量纲）又叫能量谱（密度），它描述了信号能量的频域分布。
  • 功率信号的功率谱（密度）描述了信号功率随频率的分布特点（密度：单位频率上的功率）。
  • 平稳信号功率谱密度恰好是其自相关函数的傅氏变换。
  • 对于非平稳信号，其自相关函数的时间平均（对时间积分，随时变性消失而再次退变成一维函数）与功率谱密度仍是傅氏变换对。
  • 一个信号的频谱,只是这个信号从时域表示转变为频域表示,频谱只是同一种信号的不同的表示方式而已；而功率谱是从能量的观点对信号进行的研究,其实频谱和功率谱的关系归根结底还是信号和功率,能量等之间的关系。

谱估计

  • 功率谱估计一般分成两大类：
    • 经典谱估计，也称为非参数谱估计。
    • 现代谱估计，也称为参数谱估计。

matlab功率谱估计

  • PART 1: 产生原始信号及显示
clear;clc;close all;

%% 产生原始信号
f1=5;f2=2;f3=20; f4=100;                           
fs=500;                  			       % 采样率
N=fs*60;                    			   % 采样点数
t = 0 : 1/fs : (N-1)/fs;       			   % 横坐标t坐标精度
% noise_create= randn(1,length(t));        % 产生含有噪声的序列
y1=5*sin(2*pi*f1*t)+10*sin(2*pi*f2*t)+8*sin(2*pi*f3*t)+15*sin(2*pi*f4*t); 
figure(1);subplot(2,1,1);plot(y1,'r');     % 画出原信号的时频图

%% 画出原信号的频率谱
n=0:N-1;
f=n*fs/N;                      			   % 频谱图的频率序列
y=fft(y1,N);                  			   % 对信号进行快速傅里叶变换
mag=abs(y)*2/N;                			   % 求得傅里叶变换后的振幅，与真实幅值相比需要做abs(y)*2/N的运算
subplot(2,1,2); plot(f(1:N/2),mag(1:N/2)); % 绘出Nyquist频率之前随频率变化的振幅

原始波形图及频谱图如图所示：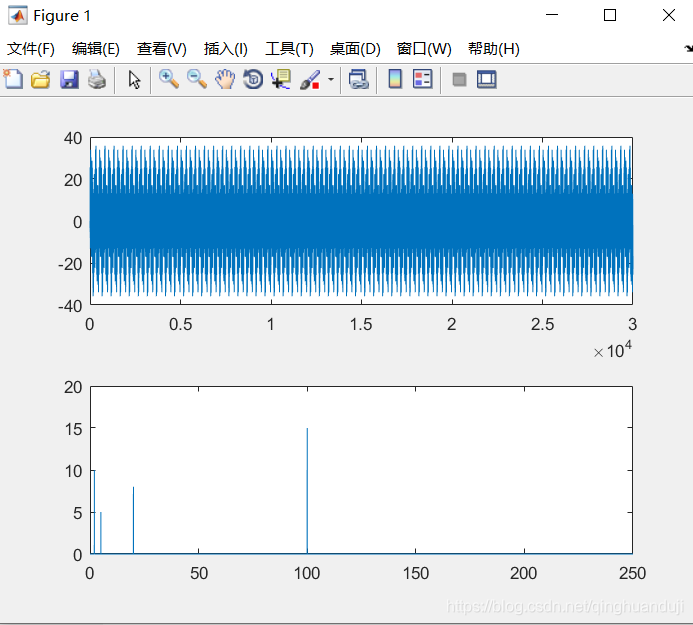
图1

  • PART 2: 直接法(周期图法)求功率谱
%%  直接法(周期图法)求功率谱
% 直接将信号的采样数据x(n)进行Fourier变换求取功率谱密度估计的方法                         
nfft=length(y1);                           % 采样的点数
window=boxcar(length(y1));                 % 使用矩形窗(默认为矩形窗，窗的大小与信号长度一样)
[Pxx,f]=periodogram(y1,window,nfft,fs);    % 直接法
figure(2);subplot(2,2,1);plot(y1);title('信号波形');
subplot(2,2,2);plot(f,10*log10(Pxx));title('周期图法原始信号的功率谱');  %绘制分贝形式的功率谱
% pxx和fft后的平方是一个量纲(w/hz)，10*log10就是用db做单位。
  • PART 3: 间接法求功率谱(先估计出自相关函数，再傅里叶变化求功率谱)
%%  间接法求功率谱(先估计出自相关函数，再傅里叶变化求功率谱)
nfft=length(y1);
cxn=xcorr(y1,'unbiased');                  % 计算序列的自相关函数
CXk=fft(cxn,nfft);
Pxx=abs(CXk);
index=0:round(nfft/2-1);
k=index*fs/nfft;
plot_Pxx=10*log10(Pxx(index+1)); 
subplot(2,2,3);plot(y1);title('信号波形');
subplot(2,2,4);plot(k,plot_Pxx);title('间接法原始信号的功率谱');     %绘制分贝形式的功率谱
图3
图2
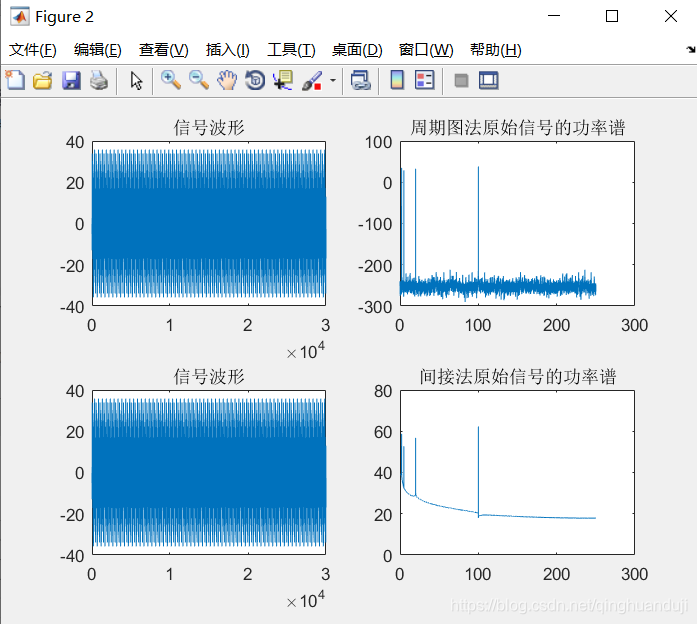
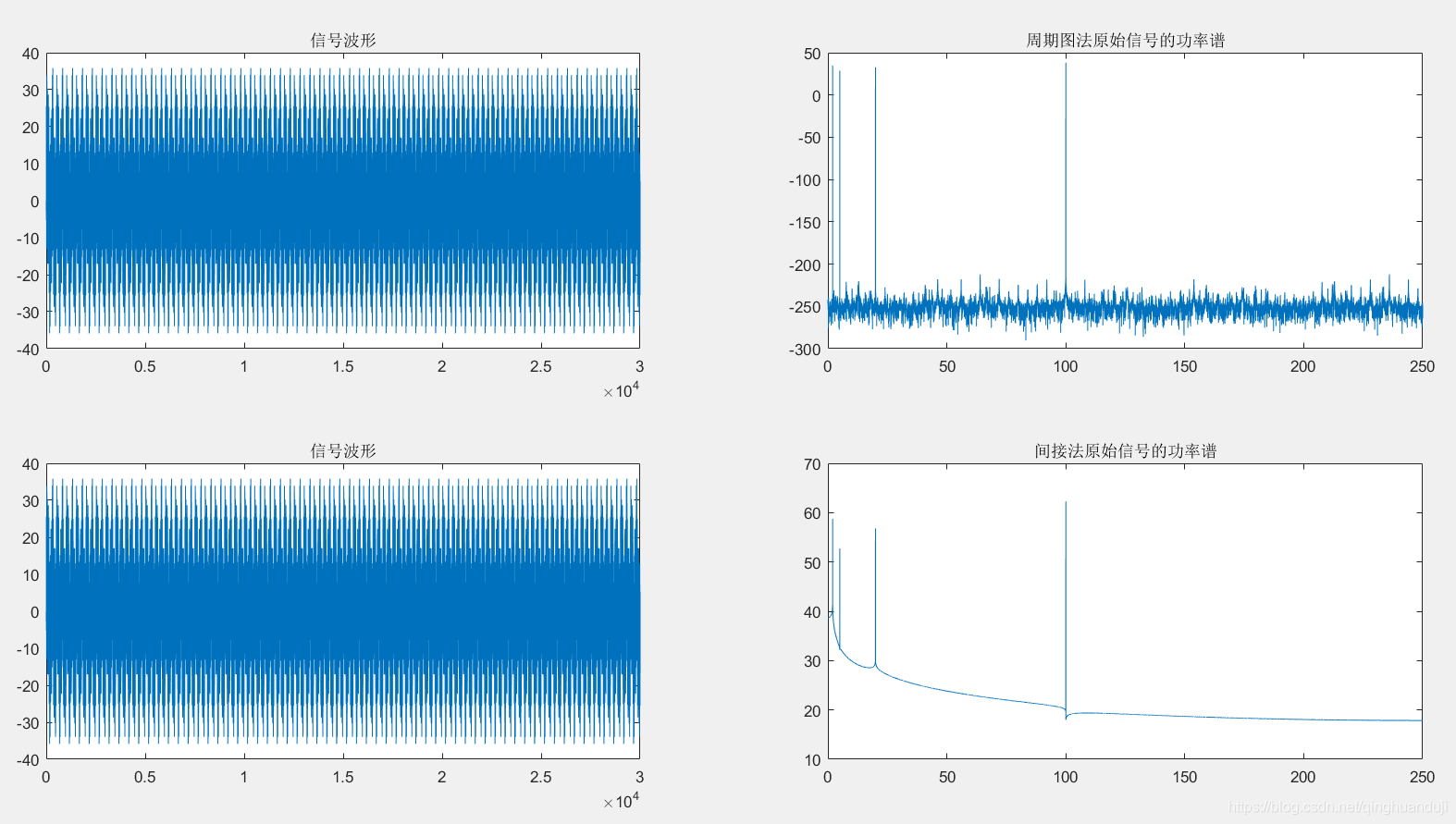
  • PART 4: 改进直接法：Bartlett法
%% 改进直接法：Bartlett法（将N点的有限长序列x(n)分段求周期图再平均。）
% 对于直接法的功率谱估计，当数据长度N太大时，谱曲线起伏加剧，若N太小，谱的分辨率又不好，因此需要改进。
nfft=length(y1);
window=boxcar(length(y1));                              %矩形窗
noverlap=0;                                            %数据无重叠
[Pxx,Pxxc]=spectrogram(y1,window,noverlap,nfft,fs);
index=0:round(nfft/2-1);
k=index*fs/nfft;
plot_Pxx=10*log10(Pxx(index+1));
plot_Pxxc=10*log10(Pxxc(index+1));
figure(4);
subplot(1,2,1);
plot(k,plot_Pxx);title('直接法信号');
subplot(1,2,2);
plot(k,[plot_Pxx plot_Pxx-plot_Pxxc plot_Pxx+plot_Pxxc]);title('Bartlett信号');
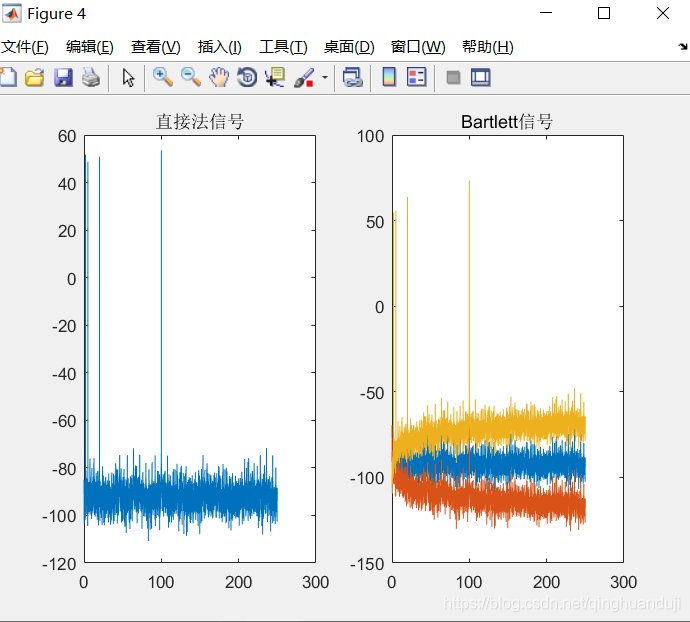
在这里插入图片描述
  • PART 5: 加窗平均周期图法 Welch法
%% 加窗平均周期图法 Welch法（选择适当的窗函数，并在周期图计算前直接加进去）
% % Welch法对Bartlett法进行了两方面的修正，一是选择适当的窗函数w(n)w(n)w(n)，并再周期图计算前直接加进去，
% % 加窗的优点是无论什么样的窗函数均可使谱估计非负。二是在分段时，可使各段之间有重叠，这样会使方差减小。
Fs=500;
n=0:1/Fs:1;
nfft=length(y1);
window=boxcar(N);                                         % 矩形窗（时间变量的零次幂窗）
window1=hamming(N);                                       % 海明窗（改进的升余弦窗） 
window2=blackman(N);                                      % blackman窗
noverlap=0;                                               % 数据无重叠
range='onesided';                                         % 频率间隔为[0 Fs/2]，只计算一半的频率
[Pxx,f]=pwelch(y1,window,noverlap,nfft,Fs,range);
[Pxx1,f1]=pwelch(y1,window1,noverlap,nfft,Fs,range);
[Pxx2,f2]=pwelch(y1,window2,noverlap,nfft,Fs,range);
plot_Pxx=10*log10(Pxx);
plot_Pxx1=10*log10(Pxx1);
plot_Pxx2=10*log10(Pxx2);
figure(5);
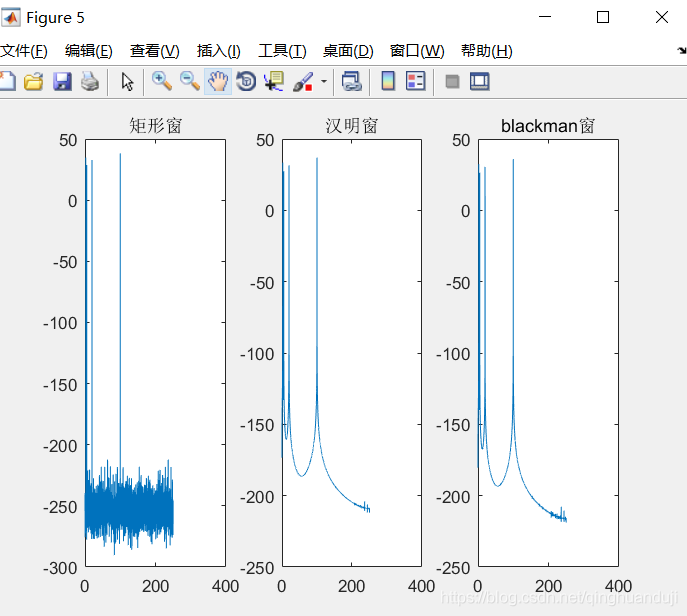
subplot(1,3,1);
plot(f,plot_Pxx);title('矩形窗');                         % 主瓣比较集中，缺点是旁瓣较高，并有负旁瓣，导致变换中带进了高频干扰和泄漏，甚至出现负谱现象。

subplot(1,3,2);                                           % 海明窗的频谱也是由3个矩形时窗的频谱合成，但其旁瓣衰减速度为20dB/（10oct）
plot(f1,plot_Pxx1);title('汉明窗');                       % (改善频率泄露)加上汉明窗，只有中间的数据体现出来了，两边的数据信息丢失了，所以等会移窗的时候，只会移1/3或1/2窗，这样被前一帧或二帧丢失的数据又重新得到了体现。

subplot(1,3,3);
plot(f2,plot_Pxx2);title('blackman窗');
在这里插入图片描述
在这里插入图片描述

注释

  • [Pxx,f] = periodogram(x,window,nfft,fs)的解释：
    • window：所使用的窗口，默认是boxcar（矩形窗），其长度必须与x的长度一致；
    • nfft(傅里叶变换长度)：采样点数。
    • fs：采样频率。
  • [S,F,T,P]=spectrogram(x,window,noverlap,nfft,fs)
    [S,F,T,P]=spectrogram(x,window,noverlap,F,fs)的解释：
    • x—输入信号的向量。默认情况下，即没有后续输入参数，x将被分成8段分别做变换处理，如果x不能被平分成8段，则会做截断处理。
    • window—窗函数，默认为nfft长度的海明窗Hamming
    • noverlap—每一段的重叠样本数，默认值是在各段之间产生50%的重叠。
    • nfft—做FFT变换的长度，默认为256和大于每段长度的最小2次幂之间的最大值。另外，此参数除了使用一个常量外，还可以指定一个频率向量F
    • fs—采样频率，默认值归一化频率。
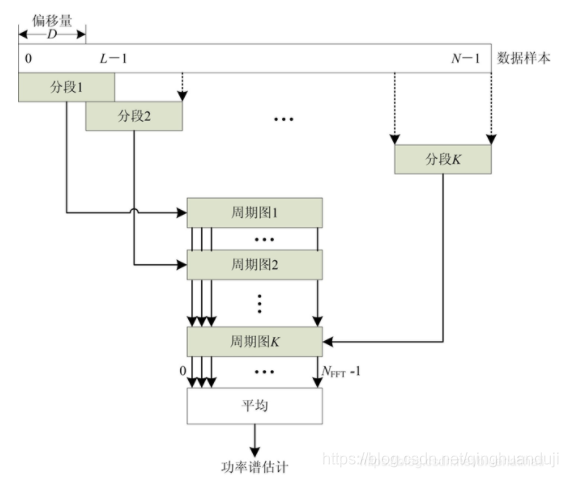
  • 周期图法改进——Bartlett方法和Welch方法：
    • Bartlett方法：D=L； Welch方法： D=L/2
    • Bartlett方法就是把数据分D段，每段fft模平方除以每段长度，再把D段的s相加再平均。
    • Welch方法就是有重复的分段，具体如下图：
      在这里插入图片描述

能量谱的介绍与代码

  • 能量谱也叫能量谱密度，能量谱密度描述了信号或时间序列的能量如何随频率分布。能量谱是原信号傅立叶变换的平方。
  • 下面是之前的一个代码（不确定是否正确）
y=fft(y1,N);               
A1=abs(y1);           
A2=A1.^2;

补充：

该部分补充内容摘自 知乎专栏 与信号处理有关的那些东东
作者Mr.括号。下为链接

信号频域分析方法的理解（频谱、能量谱、功率谱、倒频谱、小波分析）

  1. 功率谱密度的单位是什么，dB与W/Hz的介绍
    • 功率谱的单位是W/Hz，单位是dB时是做了对数处理（10logX）。
    • 取对数的目的是使那些振幅较低的成分相对高振幅成分得以拉高，以便观察掩盖在低幅噪声中的周期信号。
  2. 求功率谱的两种方法哪个好？
    • 从原理上讲似乎没什么区别，从MATLAB的结果上来看，相关函数法对噪声的抑制效果更好，图线更平滑。
  3. FFT和PSD都是表示的频谱特性，帮助我们找出峰值的位置，那么有了FFT为什么还要提出PSD？
    • 信号分为确定信号和随机信号，而确定信号又分为能量信号和功率信号，随机信号一定是功率信号。
    • 根据狄里赫利条件，能量信号可以直接进行傅里叶变换，而功率信号不行。
    • 对于无法做傅里叶变换的信号，只能走一步弯路，先求自相关，再做傅里叶。但是物理意义上就是功率谱了。不过总之得到了信号的频率特性。
  4. 既然为什么随机信号的一次FFT没有意义却还能(傅立叶变换的平方)/(区间长度)得到功率谱？
    • 对随机信号直接做FFT的做法其实就是截断成能量信号进行处理，这种处理不符合随机信号定义，但之所以这样做，是做短时频域分析下作的近似处理。
  5. 频谱和能量谱（也叫能量谱密度）是傅里叶变换得到的复数结果和模平方的关系； 而功率谱（也就是功率谱密度）是针对随机信号分析提出的概念。

发表评论