转载：C++实现多项式曲线拟合–polyfit

基本原理：幂函数可逼近任意函数。

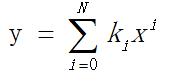
上式中，N表示多项式阶数，实际应用中一般取3或5；

假设N=5，则：

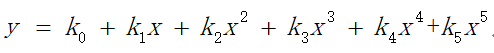
共有6个未知数，仅需6个点即可求解；

可表示为矩阵方程：

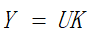
Y的维数为[R*1]，U的维数[R * 6]，K的维数[6 * 1]。

R> 6时，超定方程求解：

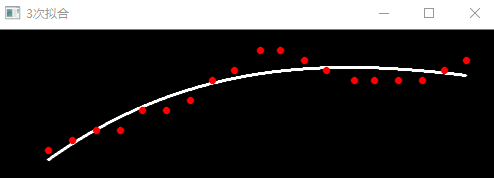
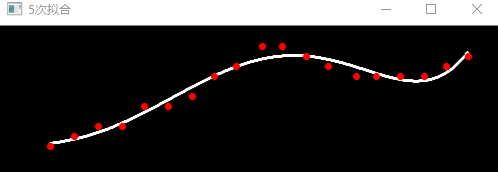
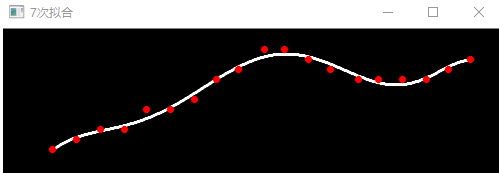
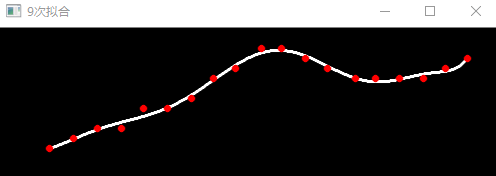
下面是使用C++实现的多项式拟合的程序，程序中使用opencv进行矩阵运算和图像显示。程序分别运行了N=3,5,7,9时的情况，结果如下：

#include <opencv2\opencv.hpp>
#include <iostream>
#include <vector>
using namespace cv;
using namespace std;
 
Mat polyfit(vector<Point>& in_point, int n);
 
int main()
{
	//数据输入
	Point in[19] = { Point(50,120),Point(74,110),Point(98,100),Point(122,100),Point(144,80)
		,Point(168,80),Point(192,70),Point(214,50),Point(236,40),Point(262,20)
		,Point(282,20),Point(306,30),Point(328,40),Point(356,50),Point(376,50)
		,Point(400,50),Point(424,50),Point(446,40),Point(468,30) };
 
	vector<Point> in_point(begin(in),end(in));
	
	//n:多项式阶次
	int n = 9;
	Mat mat_k = polyfit(in_point, n);
 
 
	//计算结果可视化
	Mat out(150, 500, CV_8UC3,Scalar::all(0));
 
	//画出拟合曲线
	for (int i = in[0].x; i < in[size(in)-1].x; ++i)
	{
		Point2d ipt;
		ipt.x = i;
		ipt.y = 0;
		for (int j = 0; j < n + 1; ++j)
		{
			ipt.y += mat_k.at<double>(j, 0)*pow(i,j);
		}
		circle(out, ipt, 1, Scalar(255, 255, 255), CV_FILLED, CV_AA);
	}
 
	//画出原始散点
	for (int i = 0; i < size(in); ++i)
	{
		Point ipt = in[i];
		circle(out, ipt, 3, Scalar(0, 0, 255), CV_FILLED, CV_AA);
	}
 
	imshow("9次拟合", out);
	waitKey(0);
	
	return 0;
}
 
Mat polyfit(vector<Point>& in_point, int n)
{
	int size = in_point.size();
	//所求未知数个数
	int x_num = n + 1;
	//构造矩阵U和Y
	Mat mat_u(size, x_num, CV_64F);
	Mat mat_y(size, 1, CV_64F);
 
	for (int i = 0; i < mat_u.rows; ++i)
		for (int j = 0; j < mat_u.cols; ++j)
		{
			mat_u.at<double>(i, j) = pow(in_point[i].x, j);
		}
 
	for (int i = 0; i < mat_y.rows; ++i)
	{
		mat_y.at<double>(i, 0) = in_point[i].y;
	}
 
	//矩阵运算，获得系数矩阵K
	Mat mat_k(x_num, 1, CV_64F);
	mat_k = (mat_u.t()*mat_u).inv()*mat_u.t()*mat_y;
	cout << mat_k << endl;
	return mat_k;
}