/*******************************************************
int *WhatSpecies;
array to specify species for each atom in the system
size: WhatSpecies[atomnum+1]
allocation: call as Allocate_Arrays(1) in Input_std.c
free: call as Free_Arrays(0) in openmx.c
*******************************************************/
int *WhatSpecies;一、哈密顿量的声明
/*******************************************************
double *****H;
Kohn-Sham matrix elements of basis orbitals
size: H[SpinP_switch+1]
[Matomnum+MatomnumF+MatomnumS+1]
[FNAN[Gc_AN]+1]
[Spe_Total_NO[Cwan]]
[Spe_Total_NO[Hwan]]
allocation: allocate in truncation.c
free: in truncation.c
and call as Free_Arrays(0) in openmx.c
*******************************************************/
double *****H;哈密顿量是密度泛函理论在算法实现中的核心。哈密顿量的构建在大多数教材中并没有详细描述。哈密顿量的构建过程与我最初的想法不同,更类似图论的意思。
看上面对H矩阵的声明,上面的这些声明都在文件openmx_common.h当中。H矩阵是一个五维的矩阵,从它各个指标的名称上,我们可以大致推断出这些维度指的具体内容。
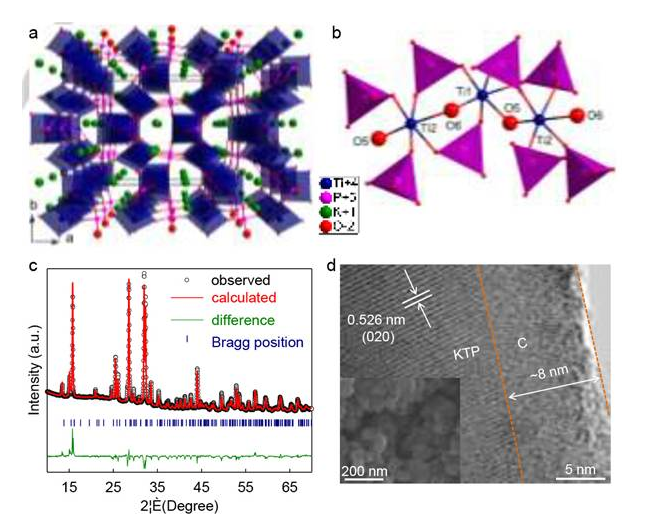
第一层SpinP_switch与自旋轨道耦合有关。在OpenMX 3.8的用户手册当中,可以找到关键字scf.SpinPolarization
scf.SpinPolarization NC # On|Off|NC非线性密度泛函理论,包括自旋轨道耦合也是在仿真中可以实现的。当进行非线性DFT时,上面这个参数就可以选择使用。
在openmx源代码中,可以找到在read_scfout.h中它出现了,它的声明是在openmx_common.h的2448行,如下图所示。

在DFT.c中,似乎可以看到上面对于SpinP_switch这个参数的印证

自旋轨道耦合这个事情太玄幻,还是少掺和。
下一个参数是Matomnum+MatomnumF+MatomnumS,这里的Matomnum代表最大原子数目的意思,后面那两个不知道是啥。作为哈密顿量,要把体系的所有原子都统计进来,这是非常合理的。
再接下来是FNAN[Gc_AN],这个FNAN是first neighboring atoms的数量,是一个数组。一个原子在空间中,总有那些离得远的或者离得近的。
/*******************************************************
int *FNAN;
the number of first neighboring atoms
size: FNAN[atomnum+1]
allocation: call as Allocate_Arrays(2) in readfile.c
free: call as Free_Arrays(0) in openmx.c
*******************************************************/
int *FNAN;记得使用OpenMX的过程中,有时候原子设置过近,要么跑不出来,要么跑得时间贼长,结果还明显不对。
FNAN意思是哈密顿量统计不了离得远的那些原子。
再接下来一个参数是Spe_Total_NO[Cwan]
/*******************************************************
int *Spe_Total_NO;
the number of primitive atomic orbitals in a species
size: Spe_Total_NO[SpeciesNum]
allocation: call as Allocate_Arrays(2) in readfile.c
free: call as Free_Arrays(0) in openmx.c
*******************************************************/
int *Spe_Total_NO;这个是指轨道数,比较好理解。
结合上面的几个指标,可以设想出这样的情形:哈密顿量计算过程中,加入一项,这一项由一个碳原子的2p轨道和一个与之相邻的氢原子的1s轨道相互作用贡献。
二、哈密顿量的构建
在文件trancation.c的低507行开始,OpenMXmalloc了众多的数组,其中就有许多来存储哈密顿量的矩阵。正式开始在538行。过程不长,所以把代码全贴出来,后面分析。
/* H0 */
size_H0 = 0;
H0 = (double*****)malloc(sizeof(double****)*4);
for (k=0; k<4; k++){
H0[k] = (double****)malloc(sizeof(double***)*(Matomnum+1));
FNAN[0] = 0;
for (Mc_AN=0; Mc_AN<=Matomnum; Mc_AN++){
if (Mc_AN==0){
Gc_AN = 0;
tno0 = 1;
}
else{
Gc_AN = M2G[Mc_AN];
Cwan = WhatSpecies[Gc_AN];
tno0 = Spe_Total_NO[Cwan];
}
H0[k][Mc_AN] = (double***)malloc(sizeof(double**)*(FNAN[Gc_AN]+1));
for (h_AN=0; h_AN<=FNAN[Gc_AN]; h_AN++){
if (Mc_AN==0){
tno1 = 1;
}
else{
Gh_AN = natn[Gc_AN][h_AN];
Hwan = WhatSpecies[Gh_AN];
tno1 = Spe_Total_NO[Hwan];
}
H0[k][Mc_AN][h_AN] = (double**)malloc(sizeof(double*)*tno0);
for (i=0; i<tno0; i++){
H0[k][Mc_AN][h_AN][i] = (double*)malloc(sizeof(double)*tno1);
size_H0 += tno1;
}
}
}
}
这里分层重复用malloc函数,每一层都定义下一层的指针,最后一层有一个二维数组收尾。
可以看到SpinP_switch这个地方的临时变量k让循环跑k=0,1,2,3这四个值,好像与SpinPolarization参数3不符,这是 个问题,以后再讨论。目前的猜想是整个H数组的0都不用,因为就在下一句它就说了FNAN[0] = 0;
当下面的for循环跑第一次时,Mc_AN=0,Gc_AN=0,可以推测:
H0[k][0] = (double)malloc(sizeof(double)(FNAN[0]+1));
H0[k][0] = (double)malloc(sizeof(double)(1));
下面的for循环就可以提前退休了。H[0][0]也就到这了。所以0,1,2,3实际上只有3个有实际空间。
当Mc_AN开始大于零的时候,才是H开始有实质内容的时候。首先就来了个M2G,从声明来看就是一个局域编号和全局编号的转换。
/*******************************************************
int *M2G
M2G gives a conversion from the medium
index to the global indicies of atoms.
size: M2G[Matomnum+1]
allocation: in Set_Allocate_Atom2CPU.c
free: call as Free_Arrays(0) in openmx.c
and in Set_Allocate_Atom2CPU.c
*******************************************************/
int *M2G;Cwan是该原子的种类,tno0是它的原子轨道数。
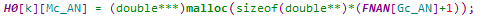
就会按需分配,有多少个最邻近原子,就分配多少个空间。
而每分配一个内存指针,都要指向一个二维数组,这也就是(**double)所指出的。
natn这个数组可能是一个地图。给定了核心原子全局序号Gc_AN和最近原子迭代临时变量h_AN就可以立即得到这个核心原子的一系列最近原子的全局编号Gh_AN。下面的工作就比较容易看懂了。
下面分两层进行malloc,最终把哈密顿量完全构建起来了。

附注
看代码还是要用Source Insight,效率提升一万倍。