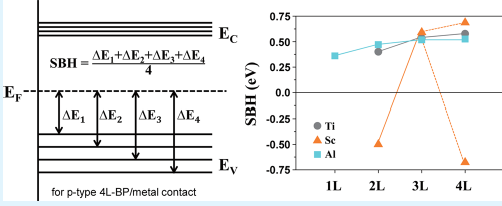
ABSTRACT: Schottky barrier height and carrier polarity are seminal concepts for a practical device application of the interface between semiconductor and metal electrode. Investigation of those concepts is usually made by a conventional method such as the Schottky−Mott rule, incorporating the metal work function and semiconductor electron affinity, or the Fermi level pinning effect, resulting from the metal-induced gap states. Both manners are, however, basically applied to the bulk semiconductor metal contacts. To explore few-layer black phosphorus metal contacts far from the realm of bulk, we propose a new method to determine the Schottky barrier by scrutinizing the layer-by-layer phosphorus electronic structure from the first-principles calculation combined with the state-of-the-art band unfolding technique. In this study, using the new method, we calculate the Schottky barrier height and determine the contact polarity of Ti, Sc, and Al metal contacts to few-layer (mono-, bi-, tri-, and quadlayer) black phosphorus. This gives a significant physical insight toward the utmost layer-by-layer manipulation of electronic properties of few-layer semiconductor metal contacts.
大体意思:原来研究肖特基势垒都是用的传统的Schotty-Mott原则,引入功函数和亲和势或者费米能级钉扎效应。现在要研究黑磷,这玩意根本就不是体材料,我们搞出来一种第一性原理的方法,轻轻松松算出来,黑磷和各种金属接触的极性。
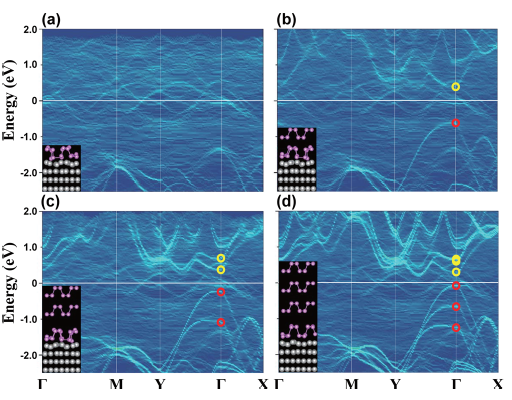
surface. Electronic band structures of (a) 1L-BP/Ti, (b) 2L-BP/Ti, (c)
3L-BP/Ti, and (d) 4L-BP/Ti systems are provided, where the effective
primitive cell projected to the BP side is recovered from the supercell
calculations. The line thickness is proportional to the weight, and the
Fermi level is set to zero. Red (yellow) empty circles at the Γ-point
indicate VBMs (CBMs) attributed to each BP layer.
Subsequently, to simulate the BP/metal contact systems, we carried out the supercell calculation due to the lattice mismatch between BP and the metal. The BP/Ti contact is composed of a rectangular 4 × 3 supercell of BP and a 3 × 2 supercell of Ti (0001), which have a 2.3 and 3.8% lattice mismatch along x- and y-axis, respectively. For the BP/Sc contact, a 5 × 1 supercell of BP and a 4 × 1 supercell of Sc (0001) were employed, leading to less than 1% lattice mismatch along both x- and y-axis. Finally, for the BP/Al contact, we used a 3 × 3 supercell of BP and a 5 × 2 supercell of Al (111), leading to 4 and 0.1% lattice mismatch along x- and y-axis, respectively. An integration over the Brillouin zone was carried out by using an 8 × 8 × 1 Monkhorst−Pack k-point mesh for the BP/Ti contact, a 1 × 8 × 1 mesh for the BP/Sc contact, and a 7 × 10 × 1 mesh for the BP/Al contact.
Band Unfolding Technique. When the period of the supercell grows longer, the first Brillouin zone of the supercell shrinks its size. Therefore, the supercell calculation meets a well-known difficulty, leading to the zone folding of the bands. Here, we overcome this difficulty using the state-of-the-art band unfolding technique36 based on the method by Popescu and Zunger.37 In the band unfolding, it is a core procedure to construct a spectral function A(k, E), an effective primitive cell projection of the supercell band structure, which could be compared with the experimental data obtained through the angleresolved photoemission spectroscopy measurement. This enables us to
obtain a primitive cell representation of a system simulated through the supercell calculation.
参考文献:
Role of Fermi-level pinning in nanotube Schottky diodes
ACS Appl. Mater. Interfaces-2017-New Method to Determine the Schottky Barrier in Few-Layer Black Phosphorus Metal Contacts