后处理部分:
Print[ e, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir, Sprintf("e_pml%g.pos", !Flag_SilverMuller)] ] ;这里的OnElementOf
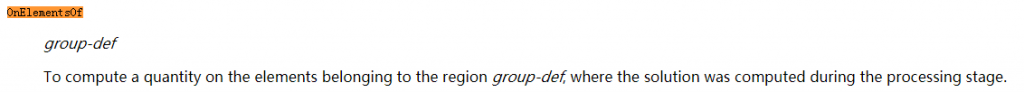
对于DefineNumber的用法:
n = DefineNumber[ 3.14, Name "a number", <attributes...>];
如果有,则用数据库原有值,这里的新值被忽略


Group{
DefineGroup[ Domain, DomainC, DomainCC, DomainS, DomainTot ] ;
DefineGroup[ SurBC, SurS, SkinFeed ] ;
TrGr = ElementsOf[ Domain, OnOneSideOf SkinFeed ];
}
Function{
DefineFunction[ ks0, js0, nxh, BC_Fct_e, dR ];
DefineFunction[ epsilon, sigma, nu ];
DefineConstant[ ZL ];
DefineConstant[ Flag_3Dmodel, Flag_Axisymmetry, Flag_SilverMuller ];
}
If(Flag_3Dmodel)
myDir = "res3d/";
ppe = "Output-e/Three-dimensional/";
ppa = "Output-av/Three-dimensional/";
ElseIf(Flag_Axisymmetry)
myDir = "resAxi/";
ppe = "Output-e/Axysymmetric/";
ppa = "Output-av/Axysymmetric/";
Else
myDir = "res2d/";
ppe = "Output-e/Axysymmetric/";
ppa = "Output-av/Axysymmetric/";
EndIf
If(Flag_Axisymmetry)
Jacobian{
{ Name JVol ; Case { { Region All ; Jacobian VolAxiSqu ; } } } // or VolAxi
{ Name JSur ; Case { { Region All ; Jacobian SurAxi ; } } }
}
Else
Jacobian {
{ Name JVol ; Case { { Region All ; Jacobian Vol ; } } }
{ Name JSur ; Case { { Region All ; Jacobian Sur ; } } }
}
EndIf
Integration {
{ Name I1 ;
Case {
{ Type Gauss ;
Case {
{ GeoElement Point ; NumberOfPoints 1 ; }
{ GeoElement Line ; NumberOfPoints 3 ; }
{ GeoElement Triangle ; NumberOfPoints 4 ; }
{ GeoElement Quadrangle ; NumberOfPoints 4 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 4 ; }
{ GeoElement Hexahedron ; NumberOfPoints 6 ; }
{ GeoElement Prism ; NumberOfPoints 6 ; }
}
}
}
}
{ Name I2 ;
Case {
{ Type Gauss ;
Case {
{ GeoElement Point ; NumberOfPoints 1 ; }
{ GeoElement Line ; NumberOfPoints 4 ; }
{ GeoElement Triangle ; NumberOfPoints 7 ; }
{ GeoElement Quadrangle ; NumberOfPoints 7 ; }
{ GeoElement Tetrahedron ; NumberOfPoints 15 ; }
{ GeoElement Hexahedron ; NumberOfPoints 34 ; }
{ GeoElement Prism ; NumberOfPoints 21 ; }
}
}
}
}
}
FunctionSpace {
//Electric field
{ Name Hcurl_e; Type Form1;
BasisFunction {
{ Name se; NameOfCoef ee; Function BF_Edge;
Support DomainTot ; Entity EdgesOf[All]; }
}
Constraint {
{ NameOfCoef ee; EntityType EdgesOf ; NameOfConstraint ElectricField; }
}
}
//Magnetic field
{ Name Hcurl_h; Type Form1;
BasisFunction {
{ Name sh; NameOfCoef he; Function BF_Edge;
Support DomainTot ; Entity EdgesOf[All]; }
}
}
{ Name Hcurl_hp; Type Form1P; // 2D case
BasisFunction {
{ Name sn; NameOfCoef hn; Function BF_PerpendicularEdge;
Support DomainTot; Entity NodesOf[All]; }
}
}
// Magnetic vector potential (a)
{ Name Hcurl_a ; Type Form1 ;
BasisFunction {
{ Name se ; NameOfCoef ae ; Function BF_Edge ;
Support DomainTot ; Entity EdgesOf[ Domain ] ; }
}
Constraint {
{ NameOfCoef ae ; EntityType EdgesOf ; NameOfConstraint MagneticVectorPotential ; }
}
}
// Electric scalar potential (v)
{ Name Hgrad_v ; Type Form0 ;
BasisFunction {
{ Name sn ; NameOfCoef vn ; Function BF_Node ;
Support DomainTot ; Entity NodesOf[ SkinDomainC ] ; }
}
Constraint {
{ NameOfCoef vn ;
EntityType NodesOf ; NameOfConstraint ElectricScalarPotential ; }
}
}
}
Formulation {
{ Name Microwave_e_BC ; // Imposing the source: circulation of e on edges
Quantity {
{ Name e; Type Local; NameOfSpace Hcurl_e; }
}
Equation {
Galerkin { [ Dof{e} , {e} ];
In SurBC; Integration I2; Jacobian JSur; }
Galerkin { [ -BC_Fct_e[] , {e} ];
In SurBC; Integration I2; Jacobian JSur; }
}
}
// Electric field formulation
{ Name Microwave_e ; Type FemEquation;
Quantity {
{ Name e; Type Local; NameOfSpace Hcurl_e; }
If(Flag_3Dmodel)
{ Name h; Type Local ; NameOfSpace Hcurl_h; }
EndIf
If(!Flag_3Dmodel)
{ Name h; Type Local ; NameOfSpace Hcurl_hp; }
EndIf
}
Equation {
Galerkin { [ nu[] * Dof{d e} , {d e} ];
In Domain; Integration I1; Jacobian JVol; }
Galerkin { DtDof [ sigma[] * Dof{e} , {e} ];
In DomainC; Integration I1; Jacobian JVol; }
Galerkin { DtDtDof [ epsilon[] * Dof{e} , {e} ];
In Domain; Integration I1; Jacobian JVol; }
Galerkin { DtDof [ js0[] , {e} ];
In DomainS; Integration I1; Jacobian JVol; }
Galerkin { DtDof [ -ks0[] , {d e} ];
In DomainS; Integration I1; Jacobian JVol; }
Galerkin { DtDof [ -nxh[] , {e} ];
In SurS; Integration I1; Jacobian JSur; }
// store magnetic field for Admitance computation (Yin)
Galerkin { [ Dof{h} , {h} ] ;
In TrGr; Jacobian JVol ; Integration I1 ; }
Galerkin { [ -I[]*nu[]*Dof{d e}/(2*Pi*Freq), {h} ] ;
In TrGr; Jacobian JVol ; Integration I1 ; }
If(Flag_SilverMuller)
Galerkin { DtDof [ Sqrt[epsilon[]*nu[]] * ( Normal[] /\ Dof{e} ) /\ Normal[] , {e} ];
In SigmaInf; Integration I1; Jacobian JSur; }
EndIf
}
}
{ Name Microwave_av ; Type FemEquation ;
Quantity {
{ Name a ; Type Local ; NameOfSpace Hcurl_a ; }
{ Name v ; Type Local ; NameOfSpace Hgrad_v ; }
If(Flag_3Dmodel)
{ Name h; Type Local ; NameOfSpace Hcurl_h; }
EndIf
If(!Flag_3Dmodel)
{ Name h; Type Local ; NameOfSpace Hcurl_hp; }
EndIf
}
Equation {
Galerkin { [ nu[] * Dof{d a} , {d a} ] ;
In Domain ; Jacobian JVol ; Integration I1 ; }
Galerkin { DtDof[ sigma[] * Dof{a} , {a} ] ;
In DomainC ; Jacobian JVol ; Integration I1 ; }
Galerkin { [ sigma[] * Dof{d v} , {a} ] ;
In DomainC ; Jacobian JVol ; Integration I1 ; }
Galerkin { DtDof[ sigma[] * Dof{a} , {d v} ] ;
In DomainC ; Jacobian JVol ; Integration I1 ; }
Galerkin { [ sigma[] * Dof{d v} , {d v} ] ;
In DomainC ; Jacobian JVol ; Integration I1 ; }
Galerkin { DtDtDof[ epsilon[] * Dof{a} , {a} ] ;
In Domain ; Jacobian JVol ; Integration I1 ; }
Galerkin { DtDof[ epsilon[] * Dof{d v} , {a} ] ;
In Domain ; Jacobian JVol ; Integration I1 ; }
Galerkin { DtDtDof[ epsilon[] * Dof{a} , {d v} ] ;
In Domain ; Jacobian JVol ; Integration I1 ; }
Galerkin { DtDof[ epsilon[] * Dof{d v} , {d v} ] ;
In Domain ; Jacobian JVol ; Integration I1 ; }
Galerkin { [ -js0[] , {a} ] ;
In DomainS ; Jacobian JVol ; Integration I1 ; }
// storing magnetic field
Galerkin { [ Dof{h} , {h} ] ;
In TrGr; Jacobian JVol ; Integration I1 ; }
Galerkin { [ -nu[]*Dof{d a}, {h} ] ;
In TrGr; Jacobian JVol ; Integration I1 ; }
If(Flag_SilverMuller)
Galerkin { DtDof [ Sqrt[epsilon[]*nu[]] * ( Normal[] /\ Dof{a} ) /\ Normal[] , {a} ];
In SigmaInf; Integration I1; Jacobian JSur; }
EndIf
}
}
}
Resolution {
{ Name Microwave_e_BC; Hidden 1;
System {
{ Name B; NameOfFormulation Microwave_e_BC; DestinationSystem A; }
}
Operation {
Generate B; Solve B; TransferSolution B;
}
}
{ Name Analysis;
System {
If(Flag_AnalysisType==0)
{ Name A; NameOfFormulation Microwave_e; Type Complex; Frequency Freq; }
EndIf
If(Flag_AnalysisType==1)
{ Name A; NameOfFormulation Microwave_av; Type Complex; Frequency Freq; }
EndIf
}
Operation {
CreateDir[Str[myDir]];
Generate A; Solve A; SaveSolution A;
If(Flag_AnalysisType==0)
PostOperation[Microwave_e];
EndIf
If(Flag_AnalysisType==1)
PostOperation[Microwave_av];
EndIf
}
}
}
PostProcessing {
{ Name Microwave_e ; NameOfFormulation Microwave_e ;
Quantity {
{ Name e ; Value{ Local{ [ {e} ] ; In DomainTot ; Jacobian JVol ;} } }
{ Name h_from_e ; Value{
Local{ [ I[]*nu[]*{d e}/(2*Pi*Freq) ] ; In Domain; Jacobian JVol; } } }
{ Name exh ; Value{ // Poynting vector
Local{ [ CrossProduct[ {e}, Conj[ I[]*nu[]*{d e}/(2*Pi*Freq)]] ] ;
In Domain ; Jacobian JVol; } } }
{ Name testdR ; Value { Local{ [ dR[] ] ; In SkinFeed ; Jacobian JSur ; } } }
{ Name Yin ; Value { //Y Admitance = G Conductance + j B Susceptance = 1/Z ;
Integral{ [ CoefGeo/delta_gap * 1/V0 * {h} * dR[] ] ;
In SkinFeed ; Jacobian JSur ; Integration I2 ; } } }
{ Name Zin ; Value { // Z = R Resistance + j X Reactance = \frac{V0}{\oint\vec{h}\cdot\vec{dl}}
Term{ Type Global; [ 1./$Yin ] ; In SkinFeed ; }
}
}
{ Name Gin ; Value { // G Conductance
Term{ Type Global; [ Re[$Yin] ] ; In SkinFeed ; } } }
{ Name Bin ; Value { // B Susceptance
Term{ Type Global; [ Im[$Yin] ] ; In SkinFeed ; } } }
// Reflexion coefficient: Gamma = (Z_in-ZL) / (Zin+ZL) = (1-Yin*ZL) / (1 + Yin*ZL) ;
// with ZL = impedance load; vacuum impedance = Z0 = 120 * Pi = Sqrt(mu0/eps0)
{ Name Gam ; Value { Term { Type Global; [ (1-ZL*$Yin)/(1+ZL*$Yin) ] ; In SkinFeed ; } } }
{ Name reGam ; Value { Term { Type Global; [ Re[$Gam] ] ; In SkinFeed ; } } }
{ Name imGam ; Value { Term { Type Global; [ Im[$Gam] ] ; In SkinFeed ; } } }
}
}
{ Name Microwave_av ; NameOfFormulation Microwave_av ;
PostQuantity {
{ Name a ; Value { Term { [ {a} ] ; In Domain ; Jacobian JVol ; } } }
{ Name v ; Value { Term { [ {v} ] ; In Domain ; Jacobian JVol ; } } }
{ Name b ; Value { Term { [ {d a} ] ; In Domain ; Jacobian JVol ; } } }
{ Name h ; Value { Term { [ nu[] * {d a} ] ; In Domain ; Jacobian JVol ; } } }
{ Name e ; Value { Term { [ -Dt[{a}]-{d v} ] ; In Domain ; Jacobian JVol ; } } }
{ Name j ; Value { Term { [ sigma[]*(-Dt[{a}]-{d v}) ] ; In DomainC ; Jacobian JVol ; } } }
{ Name exh ; Value{
Local{ [ CrossProduct[ -Dt[{a}]-{d v}, Conj[nu[]*{d a}] ] ] ;
In Domain ; Jacobian JVol; } } }
{ Name Yin ; Value { // Y Admitance = G Conductance + j B Susceptance = 1/Z ;
Integral{ [ CoefGeo/delta_gap * 1/V0 * {h} * dR[] ] ;
In SkinFeed ; Jacobian JSur ; Integration I2 ; } } }
{ Name Zin ; Value { // Z = R Resistance + j X Reactance = \frac{V0}{\oint\vec{h}\cdot\vec{dl}}
Term{ Type Global; [ 1./$Yin ] ; In SkinFeed ; } } }
{ Name Gin ; Value { // G Conductance
Term{ Type Global; [ Re[$Yin] ] ; In SkinFeed ; } } }
{ Name Bin ; Value { // B Susceptance
Term{ Type Global; [ Im[$Yin] ] ; In SkinFeed ; } } }
// Reflexion coefficient: Gamma = (Z_in-ZL) / (Zin+ZL) = (1-Yin*ZL) / (1 + Yin*ZL) ;
// with ZL = impedance load; vacuum impedance = Z0 = 120 * Pi = Sqrt(mu0/eps0)
{ Name Gam ; Value { Term { Type Global; [ (1-ZL*$Yin)/(1+ZL*$Yin) ] ; In SkinFeed ; } } }
{ Name reGam ; Value { Term { Type Global; [ Re[$Gam] ] ; In SkinFeed ; } } }
{ Name imGam ; Value { Term { Type Global; [ Im[$Gam] ] ; In SkinFeed ; } } }
}
}
}
PostOperation {
{ Name Microwave_e ; NameOfPostProcessing Microwave_e ;
Operation {
Print[ e, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir, Sprintf("e_pml%g.pos", !Flag_SilverMuller)] ] ;
Print[ h_from_e, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir,Sprintf("h_pml%g.pos", !Flag_SilverMuller)] ];
Print[ exh, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir,Sprintf("exh_pml%g.pos", !Flag_SilverMuller)] ];
Print[ Yin[SkinFeed], OnGlobal, Format FrequencyTable, StoreInVariable $Yin, File > StrCat[myDir,Sprintf("Yin_pml%g.dat", !Flag_SilverMuller)] ];
Print[ Gin, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppe,"G=re(Y)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
Print[ Bin, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppe,"B=im(Y)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
Print[ Gam, OnRegion SkinFeed, Format FrequencyTable, StoreInVariable $Gam, File > StrCat[myDir,Sprintf("Gamma_pml%g.dat", !Flag_SilverMuller)] ];
Print[ reGam, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppe,"re(Gam)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
Print[ imGam, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppe,"im(Gam)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
}
}
{ Name Microwave_av ; NameOfPostProcessing Microwave_av ;
Operation {
Print[ a, OnElementsOf Region[{Domain,-SkinFeed}], File StrCat[myDir, Sprintf("a_av_pml%g.pos", !Flag_SilverMuller)] ] ;
Print[ v, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir, Sprintf("v_av_pml%g.pos", !Flag_SilverMuller)] ] ;
Print[ e, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir, Sprintf("e_av_pml%g.pos", !Flag_SilverMuller)] ] ;
Print[ h, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir, Sprintf("h_av_pml%g.pos", !Flag_SilverMuller)] ] ;
Print[ exh, OnElementsOf Region[{Domain,-Pml}], File StrCat[myDir, Sprintf("exh_av_pml%g.pos", !Flag_SilverMuller)] ] ;
Print[ Yin[SkinFeed], OnGlobal, Format FrequencyTable, StoreInVariable $Yin, File > StrCat[myDir,Sprintf("Yin_av_pml%g.dat", !Flag_SilverMuller)] ];
Print[ Gin, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppa,"G=re(Y)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
Print[ Bin, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppa,"B=im(Y)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
Print[ Gam, OnRegion SkinFeed, Format FrequencyTable, StoreInVariable $Gam, File > StrCat[myDir,Sprintf("Gamma_av_pml%g.dat", !Flag_SilverMuller)] ];
Print[ reGam, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppa,"re(Gam)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
Print[ imGam, OnRegion SkinFeed, Format Table, SendToServer StrCat[ppa,"im(Gam)"]{0}, Color "Ivory", File StrCat[myDir,"temp.dat"] ] ;
}
}
}
DefineConstant[
R_ = {"Analysis", Name "GetDP/1ResolutionChoices", Visible 0},
C_ = {"-solve -v2", Name "GetDP/9ComputeCommand", Visible 0},
P_ = {"", Name "GetDP/2PostOperationChoices", Visible 0}
];
微带线,mstrip.pro
Include "mstrip_param.pro";
DefineConstant[
Flag_AnalysisType = { 0, Choices{0="e-formulation", 1="av-formulation"},
Name "Input/20Type of analysis", Highlight "Blue",
Help Str["- Use 'electric field formulation' to compute the EM fields created by the microstrip antenna",
"- Use 'av-potential formulation' to compute the EM fields created by the microstrip antenna"]},
Flag_BC_Type = { 1, Choices{0="Silver Muller",1="PML"},
Name "Input/20BC at infinity", Highlight "Blue"}
];
Flag_SilverMuller = (Flag_BC_Type==0) ; // 0 if PML
Flag_3Dmodel = 1 ;
Group {
SkinAntennaL = Region[{ SKINMICROSTRIP1 }] ;
SkinAntennaR = Region[{ SKINMICROSTRIP2 }] ;
SkinAntenna = Region[{ SkinAntennaL, SkinAntennaR }] ;
SkinGroundL = Region[{ SKINGROUND1 }] ;
SkinGroundR = Region[{ SKINGROUND2 }] ;
SkinGroundM = Region[{ SKINGROUND3 }] ;
SkinGround = Region[{ SkinGroundL, SkinGroundR, SkinGroundM }] ;
SkinFeed = Region[{ SKINF_TOP, SKINF_BOT, SKINF_BACK, SKINF_FRONT }];
Air = Region[{ AIR }] ;
Substrate = Region[{ SUBSTRATE }] ;
If(!Flag_SilverMuller)
Pml = Region[{ PMLX, PMLY, PMLZ }];
EndIf
If(Flag_SilverMuller)
Pml = Region[{}];
Air += Region[{ PMLX, PMLY, PMLZ }];
EndIf
SkinDomainC = Region[{ SkinAntenna, SkinGround }];
SurBC = Region[{ SkinFeed }] ;
SigmaInf = Region[{ SURFAIR }] ;
DomainCC = Region[{ Substrate, Air, Pml }] ;
DomainC = Region[{ }] ;
Domain = Region[{ DomainC, DomainCC }] ;
DomainTot = Region[{ Domain, SkinFeed, SigmaInf }] ;
}
Function {
mu0 = 4.e-7 * Pi ;
nu0 = 1/mu0 ;
ep0 = 8.854187817e-12 ;
epr = EPSILONR ;//Dielectric constant for FR4 is 4.5
epsilon [ #{Air,SkinFeed, SigmaInf} ] = ep0 ;
epsilon [ Substrate ] = epr*ep0 ;
nu [ #{Air,Substrate,SkinFeed, SigmaInf} ] = nu0 ;
mu [ #{Air,Substrate,SkinFeed, SigmaInf} ] = mu0 ;
sigma[] = 6e7 ; // Cu
I[] = Complex[0,1] ; // imaginary number
ZL = 50 ; // Ohms load resistance
PmlXmax = wT + dwT ; PmlXmin = -dwT ;
PmlYmax = hT + D2 + dhT ; PmlYmin = -D4 - hT/2 -dhT ;
PmlZmax = zb2 ; PmlZmin = zb2-5*zb2_ ;
//=========================================================================
DampingProfileX[] =
( (X[]>=PmlXmax) || (X[]<=PmlXmin) ) ?
( (X[]>=PmlXmax) ? 1 / (PmlDelta-(X[]-PmlXmax)) : 1 / (PmlDelta-(PmlXmin-X[])) ) : 0;
DampingProfileY[] =
( (Y[]>=PmlYmax) || (Y[]<=PmlYmin) ) ?
( (Y[]>=PmlYmax) ? 1 / (PmlDelta-(Y[]-PmlYmax)) : 1 / (PmlDelta-(PmlYmin-Y[])) ) : 0;
DampingProfileZ[] =
( (Z[]>=PmlZmax) || (Z[]<=PmlZmin) ) ?
( (Z[]>=PmlZmax) ? 1 / (PmlDelta-(Z[]-PmlZmax)) : 1 / (PmlDelta-(PmlZmin-Z[])) ) : 0;
cX[] = Complex[1,-DampingProfileX[]/k0] ;
cY[] = Complex[1,-DampingProfileY[]/k0] ;
cZ[] = Complex[1,-DampingProfileZ[]/k0] ;
tens[] = TensorDiag[cY[]*cZ[]/cX[],cX[]*cZ[]/cY[],cX[]*cY[]/cZ[]];
epsilon [ Pml ] = ep0 * tens[] ;
nu [ Pml ] = nu0 / tens[] ;
eta0 = 120*Pi ; // eta0 = Sqrt(mu0/eps0)
//=========================================================================
V0 = 1 ; delta_gap = D5 ;
BC_Fct_e[] = V0/delta_gap * Vector[1, 0, 0] ;
Freq = FREQ ;
dR[#{SKINF_TOP}] = Vector[0, 1, 0] ;
dR[#{SKINF_BOT}] = Vector[0, -1, 0] ;
dR[#{SKINF_BACK}] = Vector[0, 0, -1] ;
dR[#{SKINF_FRONT}] = Vector[0, 0, 1] ;
CoefGeo = 1 ;
}
Constraint {
// For e formulation
{ Name ElectricField ;
Case {
{ Region SkinFeed ; Type AssignFromResolution ; NameOfResolution Microwave_e_BC ; }
{ Region SkinDomainC ; Type Assign ; Value 0. ; }
If(!Flag_SilverMuller)
{ Region SigmaInf ; Type Assign ; Value 0. ; }
EndIf
}
}
// For av formulation
{ Name MagneticVectorPotential ;
Case {
{ Region SkinFeed ; Type Assign ; Value 0. ; }
{ Region SkinDomainC ; Type Assign ; Value 0. ; }
If(!Flag_SilverMuller)
{ Region SigmaInf ; Type Assign ; Value 0. ; }
EndIf
}
}
{ Name ElectricScalarPotential ;
Case {
{ Region SkinFeed ; Value 1-((X[]-W1)/delta_gap) ; }//FIX ME!!!
{ Region SkinAntennaL ; Value 0. ; }
{ Region SkinAntennaR ; Value 0. ; }
{ Region SkinGroundL ; Value 1. ; }
{ Region SkinGroundR ; Value 0. ; }
{ Region SkinGroundM ; Value 0. ; }
}
}
}
Include "Microwave.pro";